|
|
|
A New Interesting Way in Mathematics ---"Relative congruence"
1. ![]() integer
a,b,s. prime
integer
a,b,s. prime ![]() the
solution always exists and unique (except
the
solution always exists and unique (except ![]() ).
We can use the fractions to express congruence value, directly
).
We can use the fractions to express congruence value, directly ![]() ,
,
that is to say the fractions have congruence meaning.
2. So we can make the definition:
(1) ![]()
(2) Never can p be denomination divisor in any finite expression, otherwise
meaningless.
3. Thus the basic operation ![]() can
be used on the both sides of
can
be used on the both sides of ![]() without
any doubt, it is easy to be proved.
without
any doubt, it is easy to be proved.
4. Furthermore, we extend the above concept to real number, based on
and controlled by power expansion series, that is to say we have discovered
the concept of ![]() Relative
Congruence.
Relative
Congruence.
5. Thus we get the necessary condition 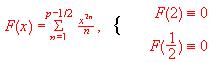 mod
p
mod
p
for 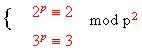 , then
we proved
, then
we proved 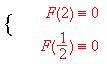 mod
p never can be satisfied with the same p.
mod
p never can be satisfied with the same p. ![]() .
.
6. And we have discussed Euler constant c, the conclusion is that c
is not rational. BACK

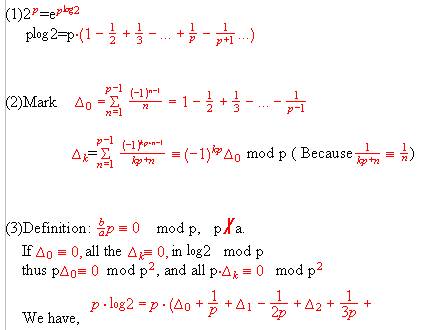 BACK
BACK
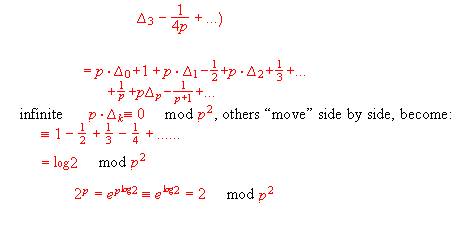 BACK
BACK


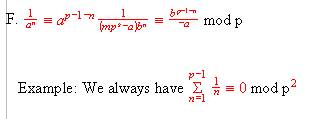 BACK
BACK



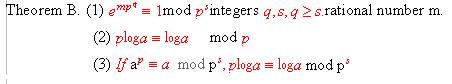 BACK
BACK
 BACK
BACK
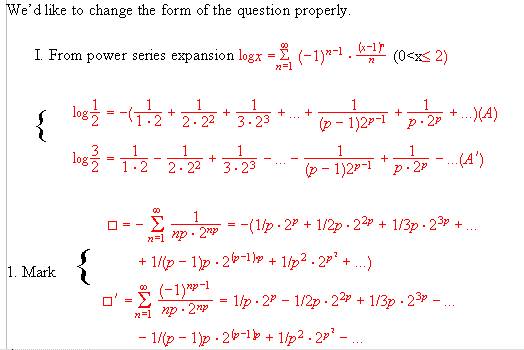 BACK
BACK
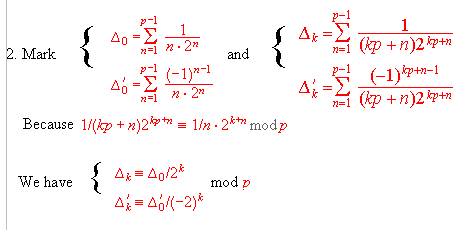
 BACK
BACK

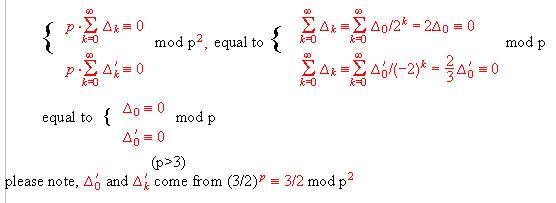
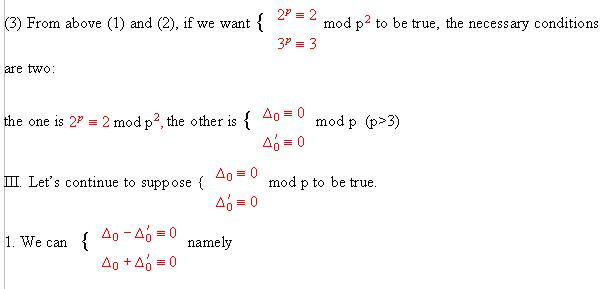
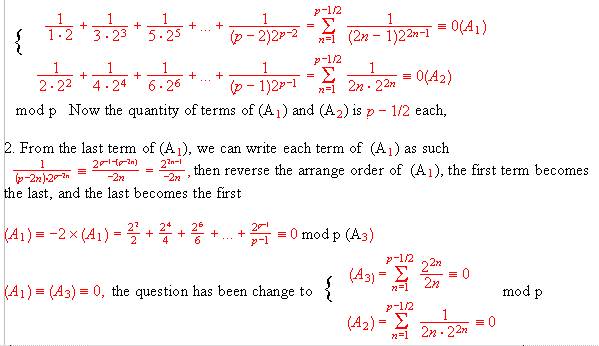
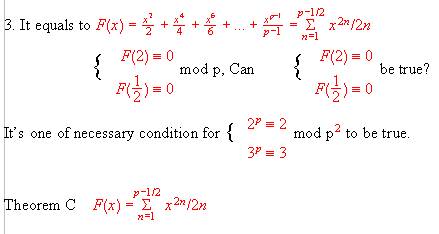 BACK
BACK



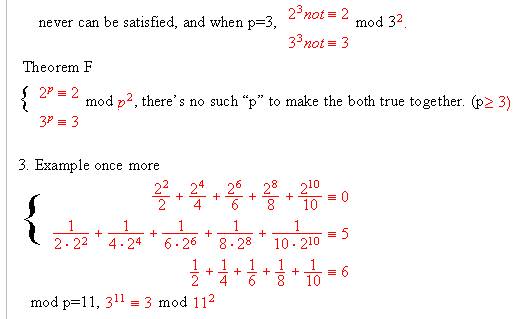 BACK
BACK

 BACK
BACK