A Letter To Mr.Clifford

	Sign In Sign-Up

A LETTER TO MR.CLIFFORD

            To: The America Mathematical Society
            Attn.: Mr. Clifford J Earle, the Managing Editor
            Fm: Li Ke Xiong
            Email: likexiong@126.com

Dear Mr. Clifford J Earle,

            I received your letter dated 8 July, many thanks.
            I think, I can and I should answer your questions, let me explain one by one.
            A. (1) I think you have already read ------
            " The Supplement of the Development of the Concept of Congruence" written by
            me.
            In this supplement, we have got the " Theorem A' ": For any P ,

            And we have checked the Theorem A' with real example p=3,5,7 and 11 in our
            paper, everything is OK. If necessary, I can go on our checking, I deeply believe
            our Theorem A' is correct. We have discovered the " structure " of ,
            for example again:
           please note if

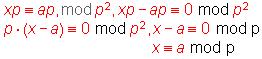
            so the above

            thus ------ this is our way.
            Let us put it in common way:

            we can see
            It is obvious the content of the two ways are totally different, though the result are
            the same.
           (2) Theorem A is the direct result from Theorem A'.
           according to our theory, we should calculate
            to see if Maybe the calculation should depend on bigger
            computer. Though we believe our Theorem A' is right and should have
            we will try our best to work it out really. [Actually, when
            n=273, that is 546/2, we can say the sum of 1/n (n from 1 to 273) congruent 0.
            mod p]
           (3) I think, it's more convenient for you to use some bigger computer to check our
            theory, if you are willing to do so, we thank you in advance.

           B. About the example on page 4 of our paper, you are right, sorry, it's my
           careless. We should set p>3, thus everything will be OK. Actually, this is
           " Wolstenholme Theorem ", we merely use our theory to re-prove it, just as a test
           for our theory.

           C. About the Part B of my definition, we totally accept your advice. The sentence
           " Will have certain meanings " should be changed. We should use " the
            congruent " instead of " certain ", to avoid vagueness.

           D. According to our Definition I (B) on page 3: Never can " p " be as the
           denominator divisor of any finite expression, otherwise meaningless, we re-write
           our Theorem B(1) on page 4 as follows:
            integers k, m, q, s.

Thank you for your precious directions, many many thanks from my heart. Please
continue with your precious instructions, let's make new discovery together.

Best Regards

Li Kexiong, July 18th, 1999