|
|
The " Primary Proof " For Fermat Last Theorem
A. At the beginning, we think it is necessary to repeat our Definitions
in the paper of " The Development of the Concept of Congruence "
Definition I (A).
mod 
.
integer a, b, n and s. 
(B). Never can "p" be as the denominator divisor of (and in) any finite
expression,
otherwise meaningless. (In any finite expressions, when "p" is a
denominator divisor,
1/p is 1/0, hence the finite expression is meaningless, mod .
We should say, if A is a basic fact, B should be true, too. A and B can
not be
separated.
B. Now, suppose 
can
be true with same p. 
We have 
,
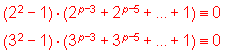
make the function f(x)=
the above two expressions are 
,
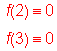
p>3.
C.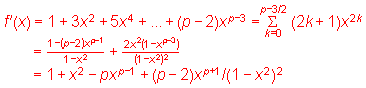 
D. Because 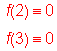(p>3)
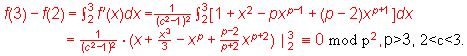
E. Let us see the above ( )
,
if ( )
p>3, surely ( )
mod p.
if suppose (
)not
mod p, ( )not
without any doubt.
a. So let us suppose (
)
mod p, we have ( )
,
please note 
when
x is an integer, 
mod p.
thus (
)
=
-2/3(27-8)=-2/3X19
mod p (p>3)
The only possibility for (
)
(p>3) is p=19.
b.Let us suppose (
)
(p>3)
(
)=
due to having supposed 
so (
)3+9-3+(p-2)/(p+2)X27-[2+8/3-2+(p-2)/(p+2)X8]
=19[1/3+(p-2)/(p+2)]
(p>3)
1. If p=19, we get
1/3+(19-2)/(19+2)
mod 19, we get 24,
or 1/3+(19-2)/(19+2)1/3+(-2)/2=1/3-1=(-2)/3mod
19.
This is a contradiction.
2. If 
,
we get 1/3+(p-2)/(p+2),
p>3 surely 1/3+(p-2)/(p+2),
that is
1/3-1
mod p [Please note: (p-2)/(p+2)
-1 ,pod p], so -2/3
mod p, p>3
-2
mod p, obviously this is also a contradiction.
F. Let us see 
,
a. Let us suppose
mod p 
k,m and s are integers 
1
s1, 
.
We know 
should be a rational number, otherwise can not match
f(3)-f(2) is rational. So
we can write
b. Needless to say
is also a meaningless one.
G. From the above E and F, we can see f(3)-f(2) never ,
. The conclusion is: there is
no such "p" to make ,
p>3 to be true together at the same time.
Site Owner: Li Ke Xiong
Email: likexiong@126.com
ALL RIGHTS RESERVED